rusiop.blogg.se - Ibm spss statistics 19 testversion

Reversely, (partial) eta-squared is the only effect size measure we obtain if we actually run the ANOVA in SPSS. The aforementioned output includes none of those. But for some weird reason, SPSS reports the “root-mean-square standardized effect” as its effect size measure.Ĭommon effect size measures for ANOVA are Sample size calculation output example from SPSS 27įortunately, the SPSS and GPower conclusions are almost identical. Note that the GPower dialog also contains the main output: we should collect data on a total sample size of N = 148 independent observations. However, you can optionally compute effect size from these numbers and proceed from there. It does not require 4 (unknown) means and an (unknown) standard deviation. Such estimated effect sizes can be directly entered in G*Power as shown below. And because it's a single number, we can consult simple rules of thumb such as So how does effect size make that situation any better? Well, first off, effect size is a single number as opposed to the separate numbers required by the dialog. The problem is that you probably won't have a clue what to enter here: since we run this analysis before collecting any data, we can't look up the required statistics. Instead, SPSS will compute it for us if we enter all expected means and the expected Pooled population standard deviation. We can't enter any effect size in this dialog. Our sample size calculation requires just one more number: the expected effect size. In the dialog that opens (below), we'll select “Estimate sample size” we'll enter the power or (1 - β) we desire we'll enter the alpha level or α at which we're planning to test. We'll first open the power analysis dialog as shown below. Now let's say we want to know the required sample size for a 4-way ANOVA. SPSS 27 - Power & Sample Size Calculations Given this scenario, we should use a total sample size of N = 157 participants as shown below. We guess that the effect size, Cohen’s f = 0.25 (medium). We're planning a 3-group ANOVA at α = 0.05 and we want (1 - β) = 0.80. So let's say we want compare 3 different medicines.

computing power for different sample sizes given a chosen α and (1 - β).

computing required sample sizes for different effect sizes given a chosen α and (1 - β).

These result in different scenarios that can easily be calculated. In practice, we usually don't know these but we can still make educated guesses. We can compute each of these 4 statistics if we know the other 3.

sample size is the number of independent observations involved in some significance test.

effect size is a standardized number that summarizes to what extent some null hypothesis is not true -either in a sample or a population.

(1 - β) or power -often 0.80- is the probability of rejecting some null hypothesis given some exact alternative hypothesis, often expressed as an effect size.

α -often 0.05- is the probability of making a Type I error: rejecting some null hypothesis if it's actually true.

Power & Sample Size Calculations - The Basicsīefore we turn to power calculations in SPSS 27, let's first revisit some minimal basics.Ĭomputing power or required sample sizes involves 4 statistics:

Cohen’s D is called “Cohen’s d” rather than “Point estimate”.

JASP reports all results in a single table.

we can choose which confidence interval it reports -optionally none.

JASP allows us to choose which effect size measure it reports.

So what makes this better than the SPSS implementation? Well, The figure below shows how it implements Cohen’s D. I'll bet a monthly salary that the “Standardizer” instead of the “Point estimate” will be reported as Cohen’s D on a pretty regular basis.

Meeting this standard requires copy-pasting results from separate SPSS tables manually -never a good idea. The APA reporting guidelines ask for a single table containing the significance tests and Cohen’s D.Sadly, this results in a separate table that contains way more output than we typically want. The only way to obtain Cohen’s D is selecting “Estimate effect sizes”. However, SPSS 27 finally includes it as shown below. SPSS users have been complaining for ages about Cohen’s D being absent from SPSS. SPSS 27 - Power & Sample Size CalculationsĬohen’s D is the main effect size measure for all 3 t-tests:.This review quickly walks you through the main improvements and their limitations. Although it has some useful new features, most of these have been poorly implemented. On 19 June 2020, SPSS version 27 was released.

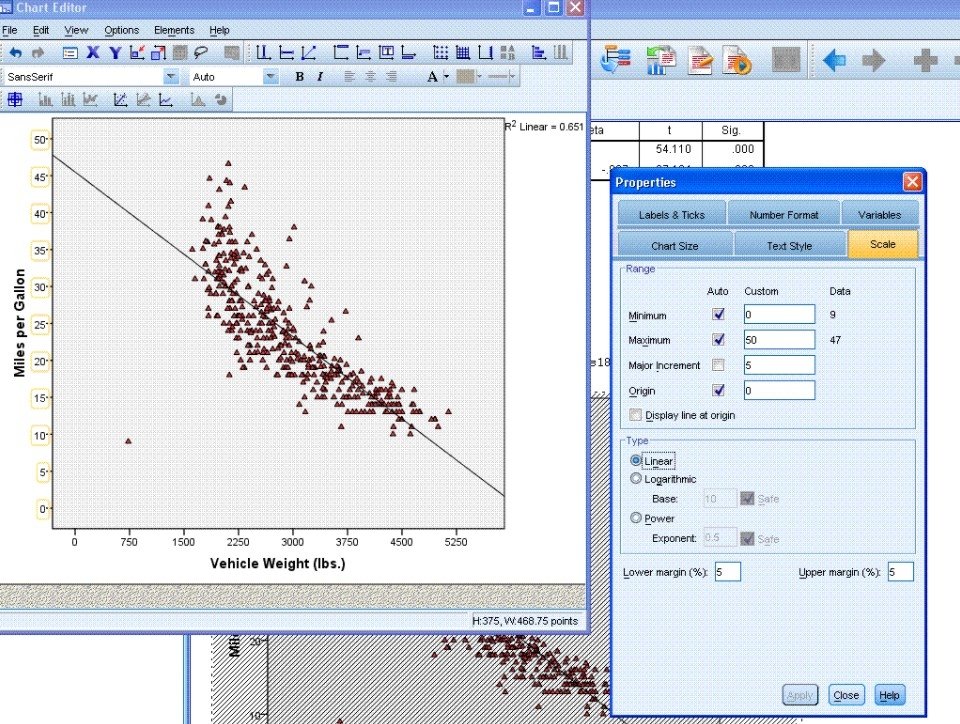
SPSS 27 – Quick Review By Ruben Geert van den Berg under SPSS Blog